13 10 As A Decimal
timefordiamonds
Sep 20, 2025 · 5 min read
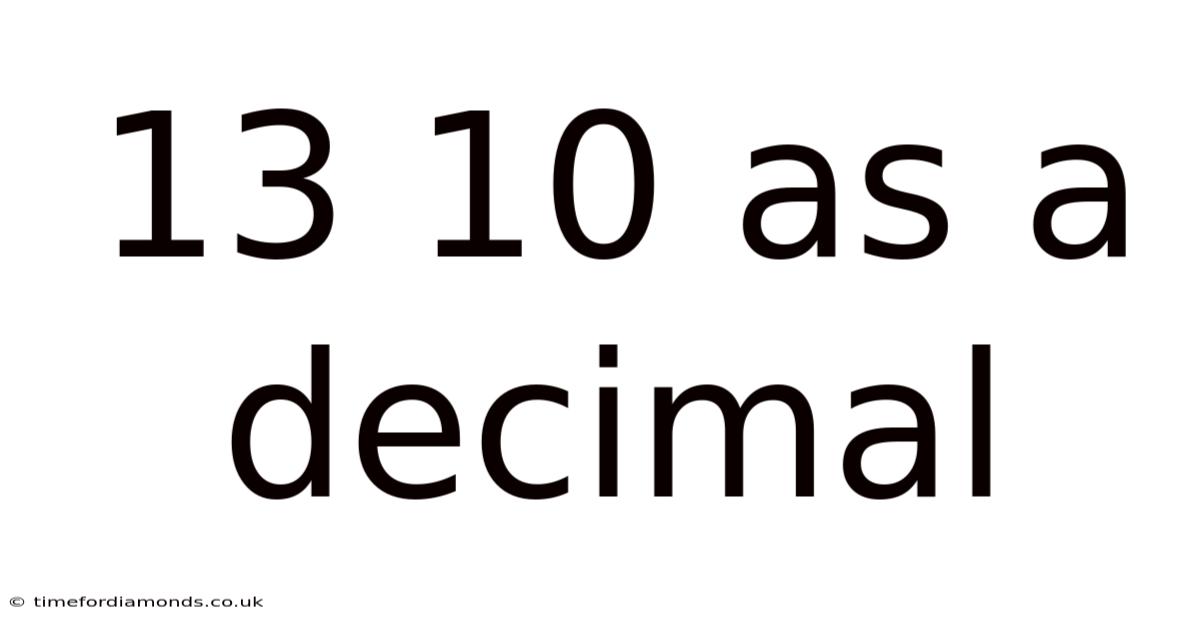
Table of Contents
13/10 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will delve into the conversion of the fraction 13/10 to its decimal equivalent, exploring the process, underlying principles, and practical applications. We'll also address common misconceptions and provide helpful tips for tackling similar conversions. This guide aims to build a strong understanding, making you confident in handling fraction-to-decimal conversions.
Introduction: Understanding Fractions and Decimals
Before diving into the specific conversion of 13/10, let's establish a foundational understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a part of a whole using base-ten notation, where a decimal point separates the whole number part from the fractional part.
Converting 13/10 to a Decimal: The Simple Method
The conversion of 13/10 to a decimal is relatively straightforward. Remember that a fraction essentially represents a division problem. The numerator (13) is divided by the denominator (10).
13 ÷ 10 = 1.3
Therefore, 13/10 as a decimal is 1.3.
Deeper Dive: Understanding the Process
The simplicity of this particular conversion belies the underlying mathematical principles. Let's break down why this works:
-
Place Value in Decimals: The decimal system is based on powers of 10. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. In the number 1.3, the '1' represents one whole unit, and the '3' represents three-tenths (3/10).
-
Dividing by Powers of 10: Dividing by 10, 100, 1000, etc., is equivalent to moving the decimal point to the left. Since 13 is a whole number, we can imagine it as 13.0. Dividing by 10 moves the decimal point one place to the left, resulting in 1.3.
-
Fractions as Division: The core concept is that a fraction always represents division. The numerator is divided by the denominator. This holds true for any fraction, regardless of its complexity.
Converting Other Fractions to Decimals
While converting 13/10 is straightforward, let's extend our understanding to other fraction-to-decimal conversions. Here's a breakdown of different scenarios:
-
Proper Fractions (Numerator < Denominator): These fractions always result in a decimal less than 1. For example, 3/4 = 0.75, 1/2 = 0.5
-
Improper Fractions (Numerator ≥ Denominator): These fractions result in a decimal greater than or equal to 1. Our example, 13/10, falls into this category. Another example: 7/2 = 3.5
-
Fractions with Larger Denominators: Converting fractions with larger denominators might require long division. For example, converting 22/7 (an approximation of π) requires a longer division process, resulting in a non-terminating decimal (3.142857...).
-
Repeating Decimals: Some fractions, when converted to decimals, result in repeating decimals. For example, 1/3 = 0.333... (the 3 repeats infinitely). These are often represented with a bar over the repeating digit(s) (e.g., 0.3̅).
Practical Applications: Where is this Knowledge Useful?
The ability to convert fractions to decimals is crucial in various real-world applications:
-
Measurement and Units: Many measurements involve fractions (e.g., inches, centimeters). Converting them to decimals often simplifies calculations.
-
Financial Calculations: In finance, dealing with percentages and proportions is common. Converting fractions to decimals helps in calculating interest, discounts, and other financial figures.
-
Science and Engineering: In scientific and engineering fields, precision is paramount. Converting fractions to decimals provides a more precise representation of measurements and calculations.
-
Data Analysis: Data analysis often involves working with numerical data, where fractions need to be converted to decimals for computations and interpretations.
-
Computer Programming: Computers work with numerical data in decimal format. Therefore, converting fractions to decimals is essential in programming applications that handle numerical computations.
Common Misconceptions and Troubleshooting
Here are some common misconceptions to avoid when converting fractions to decimals:
-
Incorrect Division: Ensure you're dividing the numerator by the denominator, not the other way around.
-
Decimal Placement: Pay close attention to the placement of the decimal point in the result. A misplaced decimal point drastically changes the value.
-
Rounding Errors: When dealing with non-terminating decimals, you might need to round the result to a specific number of decimal places. Be aware of potential rounding errors and their impact on calculations.
Frequently Asked Questions (FAQs)
-
Q: Can all fractions be converted to decimals?
- A: Yes, all fractions can be converted to decimals. However, some will result in non-terminating or repeating decimals.
-
Q: What if the denominator is not a power of 10?
- A: You can still perform long division to obtain the decimal equivalent. Alternatively, you can find an equivalent fraction with a denominator that is a power of 10.
-
Q: How do I convert a decimal back to a fraction?
- A: The process involves writing the decimal as a fraction with a denominator that is a power of 10 (e.g., 0.25 = 25/100), then simplifying the fraction.
-
Q: Are there any online tools or calculators to help with fraction-to-decimal conversion?
- A: Yes, many online calculators and tools are available that can quickly convert fractions to decimals.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a valuable mathematical skill with wide-ranging applications. Understanding the underlying principles of fractions, decimals, and division is crucial for accurate and efficient conversions. The simple conversion of 13/10 to 1.3 serves as a solid foundation for understanding more complex conversions. By mastering this skill, you'll enhance your problem-solving capabilities in various academic and real-world scenarios. Remember to practice regularly, and don't hesitate to utilize available resources to reinforce your understanding. With consistent effort, you’ll become proficient in handling fraction-to-decimal conversions with confidence and accuracy.
Latest Posts
Latest Posts
-
How Long Is 65 Feet
Sep 20, 2025
-
154 Miles To Km H
Sep 20, 2025
-
4 Ft By 8 Ft
Sep 20, 2025
-
How Fast Is One Mach
Sep 20, 2025
-
148cm To Feet And Inches
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 13 10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.