3 19/100 As A Decimal
timefordiamonds
Sep 20, 2025 · 5 min read
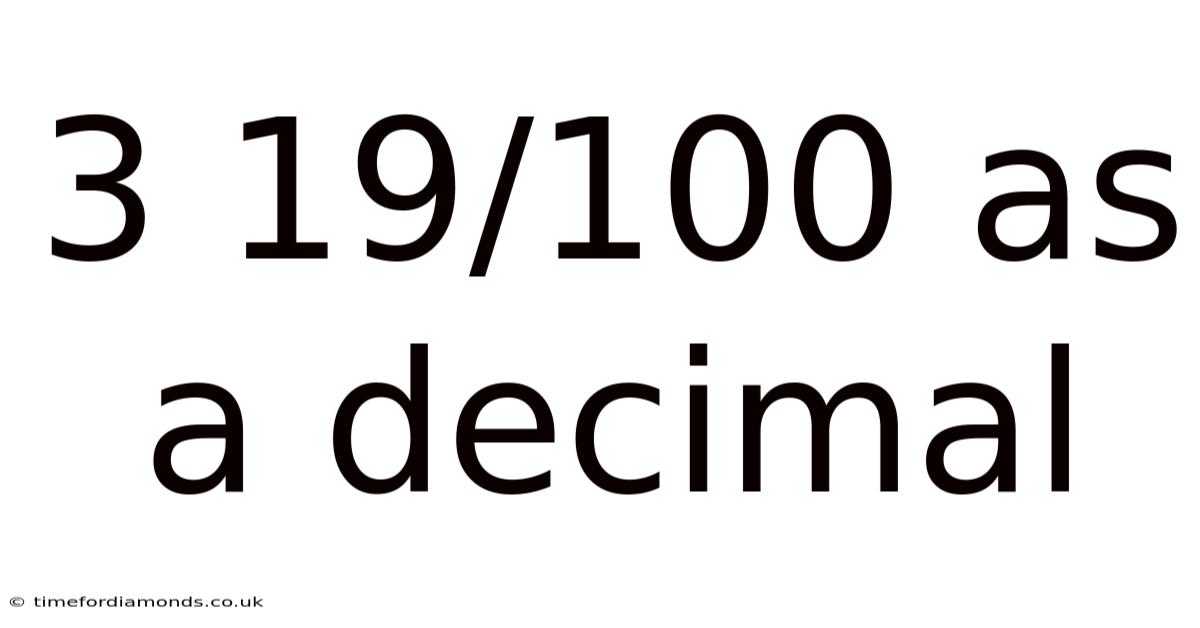
Table of Contents
Understanding 3 19/100 as a Decimal: A Comprehensive Guide
This article will thoroughly explore how to convert the mixed number 3 19/100 into its decimal equivalent. We'll break down the process step-by-step, explaining the underlying mathematical principles and offering practical examples. Understanding this conversion is crucial for various applications in math, science, and everyday life. We will also delve into the significance of decimal representation, its advantages, and its uses in different contexts.
Introduction: Decimals and Mixed Numbers
Before diving into the conversion, let's refresh our understanding of decimals and mixed numbers. A decimal is a number expressed in the base-10 numeral system, using a decimal point to separate the integer part from the fractional part. For example, 3.14 is a decimal number where 3 is the integer part and .14 is the fractional part.
A mixed number, on the other hand, combines a whole number and a fraction. 3 19/100 is a mixed number where 3 is the whole number and 19/100 is the fraction. The fraction indicates a part of a whole, in this case, 19 out of 100 equal parts.
The process of converting a mixed number to a decimal involves transforming the fractional part into its decimal equivalent and then adding it to the whole number.
Converting 3 19/100 to a Decimal: A Step-by-Step Guide
The conversion of 3 19/100 to a decimal is relatively straightforward due to the denominator (100). Denominators that are powers of 10 (10, 100, 1000, etc.) make the conversion particularly easy.
Step 1: Understanding the Fraction
The fraction 19/100 represents 19 parts out of a total of 100 equal parts. This can also be interpreted as 19 hundredths.
Step 2: Converting the Fraction to a Decimal
Since the denominator is 100, we can directly express the fraction as a decimal by placing the numerator (19) two places to the right of the decimal point. This is because 100 has two zeros. Therefore, 19/100 = 0.19.
Step 3: Combining the Whole Number and the Decimal
Now, we simply add the whole number (3) to the decimal equivalent of the fraction (0.19). This gives us: 3 + 0.19 = 3.19
Therefore, 3 19/100 as a decimal is 3.19.
Alternative Method: Converting to an Improper Fraction
An alternative method involves first converting the mixed number into an improper fraction and then converting that improper fraction into a decimal.
Step 1: Converting to an Improper Fraction
To convert 3 19/100 to an improper fraction, we multiply the whole number (3) by the denominator (100) and add the numerator (19). This result becomes the new numerator, while the denominator remains the same.
(3 * 100) + 19 = 319
So, the improper fraction is 319/100.
Step 2: Converting the Improper Fraction to a Decimal
Now, we divide the numerator (319) by the denominator (100):
319 ÷ 100 = 3.19
Again, we arrive at the same decimal equivalent: 3.19
The Significance of Decimal Representation
The decimal representation of numbers offers several advantages over fractional representation:
-
Ease of Comparison: Comparing decimals is often easier than comparing fractions, particularly when the fractions have different denominators. For instance, comparing 3.19 to 3.20 is immediately clear, whereas comparing 3 19/100 to 3 20/100 might require some calculation.
-
Computational Ease: Decimal numbers simplify arithmetic operations, especially addition, subtraction, multiplication, and division. Calculations with decimals are generally more straightforward than with fractions.
-
Wide Applicability: Decimals are widely used in various fields like science, engineering, finance, and everyday life (e.g., currency, measurements). Their consistent and easily understandable format allows for efficient communication and data representation.
-
Accuracy in Measurement: Many measurements, particularly those involving tools like rulers and scales, are expressed in decimals, offering precise and readily comparable figures.
Practical Applications of Decimal Numbers
Decimal numbers are fundamental to numerous aspects of our lives:
-
Finance: Monetary values are almost universally expressed using decimals (e.g., $3.19). Calculations involving interest, taxes, and other financial aspects heavily rely on decimal arithmetic.
-
Science and Engineering: Measurements of various quantities (length, weight, temperature, etc.) are often recorded using decimals, ensuring accuracy and precision in scientific and engineering applications.
-
Computer Science: Computers represent numbers internally using binary systems, but the output and user interface often utilize decimal representation for ease of understanding.
-
Data Analysis and Statistics: Statistical analysis frequently involves decimal numbers, allowing for accurate calculations and representation of data.
Frequently Asked Questions (FAQs)
Q1: Can all fractions be easily converted to decimals?
No, not all fractions can be easily converted to terminating decimals. Fractions with denominators that are not factors of powers of 10 (e.g., 1/3, 1/7) will result in repeating or non-terminating decimals (e.g., 0.333..., 0.142857142857...).
Q2: What if the denominator is not a power of 10?
If the denominator isn't a power of 10, you can either simplify the fraction if possible, or perform long division to convert the fraction into a decimal.
Q3: What is the difference between a terminating and a non-terminating decimal?
A terminating decimal has a finite number of digits after the decimal point (e.g., 3.19). A non-terminating decimal has an infinite number of digits after the decimal point, either repeating (e.g., 0.333...) or non-repeating (e.g., π = 3.14159...).
Q4: How can I convert a repeating decimal back to a fraction?
Converting a repeating decimal back to a fraction involves algebraic manipulation. The specific method depends on the pattern of repetition.
Conclusion: Mastering Decimal Conversions
Converting a mixed number like 3 19/100 to its decimal equivalent (3.19) is a fundamental skill in mathematics. Understanding this process is crucial for tackling more advanced mathematical concepts and solving real-world problems in various disciplines. The ease and consistency of decimal representation make it the preferred format for many applications, showcasing its importance in everyday life and professional fields. By mastering this fundamental conversion, you build a solid foundation for further mathematical explorations and problem-solving. Remember to practice regularly to solidify your understanding and improve your speed and accuracy in converting between fractions and decimals.
Latest Posts
Latest Posts
-
Cuantos Mililitro Tiene Un Litro
Sep 20, 2025
-
84 Degrees F To C
Sep 20, 2025
-
34 Stone Vs 57 Stone
Sep 20, 2025
-
31 Cm Convert To Inches
Sep 20, 2025
-
80 F Is What C
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 19/100 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.