1 3 4 To Mm
timefordiamonds
Sep 15, 2025 · 5 min read
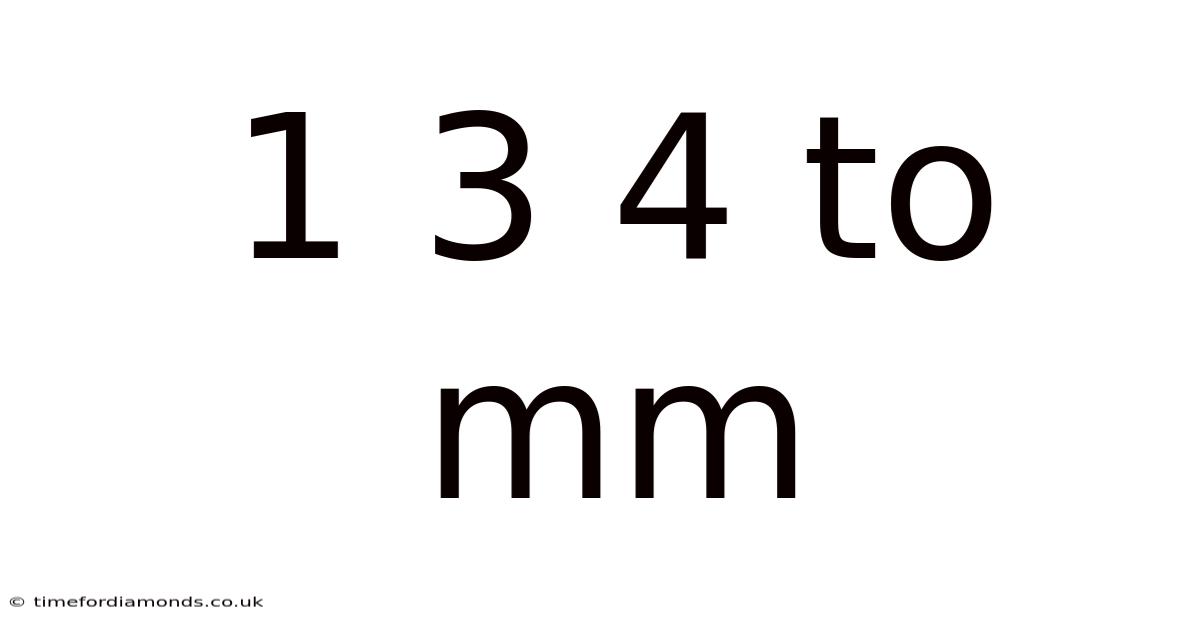
Table of Contents
Converting 1:3:4 Ratios to Millimeters: A Comprehensive Guide
Understanding how to convert ratios, especially those involving spatial dimensions like 1:3:4, into concrete measurements like millimeters (mm) is crucial in various fields, from architecture and engineering to woodworking and model making. This comprehensive guide will walk you through the process, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore different scenarios and address common questions, ensuring you're equipped to tackle any ratio-to-millimeter conversion with confidence.
Understanding Ratios and Proportions
Before diving into the conversion, let's clarify the fundamentals. A ratio, like 1:3:4, expresses the proportional relationship between different quantities. In this case, it signifies that for every one unit of the first quantity, there are three units of the second and four units of the third. These units could represent anything: length, width, height, volume – the context determines their meaning. The key is that the relative sizes are defined by the ratio. To convert this ratio to millimeters, we need an additional piece of information: a scale or the actual measurement of one of the quantities.
The Missing Piece: Establishing a Scale
The ratio 1:3:4 on its own is insufficient for a millimeter conversion. We need to know the actual size of at least one of the three dimensions. For example:
- Scenario 1: "A rectangular prism has dimensions in the ratio 1:3:4, and its shortest side is 10mm long."
- Scenario 2: "A model building has dimensions proportional to 1:3:4, and its longest side measures 40mm."
In both scenarios, the provided information establishes a scale. This scale allows us to determine the actual size of the other dimensions.
Step-by-Step Conversion: Method 1 (Using Proportions)
This method utilizes the power of proportional reasoning. Let's use Scenario 1 as our example.
1. Identify the known values:
- Ratio: 1:3:4
- Shortest side (corresponding to the '1' in the ratio): 10mm
2. Set up proportions:
We can set up three separate proportions, one for each dimension:
- Shortest side: 1/x = 10/10 (x = 10mm)
- Medium side: 3/x = 10/10 (Solving for x gives us the medium side length)
- Longest side: 4/x = 10/10 (Solving for x gives us the longest side length)
3. Solve for the unknowns:
- Shortest side (x): 1/x = 10/10 => x = 10mm
- Medium side (x): 3/x = 10/1 => x = 30mm
- Longest side (x): 4/x = 10/1 => x = 40mm
Therefore, the dimensions of the rectangular prism are 10mm x 30mm x 40mm.
Step-by-Step Conversion: Method 2 (Using a Scale Factor)
This method is more concise. It involves calculating a scale factor that converts the ratio units to millimeters. Let's use Scenario 2 (longest side = 40mm).
1. Identify the known values:
- Ratio: 1:3:4
- Longest side (corresponding to '4' in the ratio): 40mm
2. Calculate the scale factor:
The longest side in the ratio is 4 units. It corresponds to 40mm in reality. Therefore, the scale factor is 40mm / 4 units = 10mm/unit. This means each unit in the ratio represents 10mm.
3. Apply the scale factor:
Multiply each part of the ratio by the scale factor:
- Shortest side: 1 unit * 10mm/unit = 10mm
- Medium side: 3 units * 10mm/unit = 30mm
- Longest side: 4 units * 10mm/unit = 40mm
Again, we arrive at the dimensions 10mm x 30mm x 40mm.
Working with Different Units
The principles remain the same even if the given measurement isn't in millimeters. Let's say the shortest side in Scenario 1 is 1 inch (approximately 25.4mm).
1. Convert to a common unit:
First, convert 1 inch to millimeters: 1 inch * 25.4mm/inch = 25.4mm
2. Apply either Method 1 or Method 2:
Using Method 2 (scale factor):
- Scale factor: 25.4mm / 1 unit = 25.4mm/unit
- Shortest side: 1 unit * 25.4mm/unit = 25.4mm
- Medium side: 3 units * 25.4mm/unit = 76.2mm
- Longest side: 4 units * 25.4mm/unit = 101.6mm
The dimensions would be approximately 25.4mm x 76.2mm x 101.6mm.
Handling Complex Scenarios
The methods described above can be adapted to more complex scenarios involving multiple ratios or non-rectangular shapes. The key is always to establish a known relationship (a scale) between the ratio units and a real-world measurement.
For example, imagine a triangular prism where the base sides are in a 1:3 ratio and the height is four times the shortest base side. If the shortest base side is 5cm (50mm), you would:
- Convert the shortest base side to mm (already done).
- Calculate the longer base side using the 1:3 ratio.
- Calculate the height using the information that it's four times the shortest base side.
Frequently Asked Questions (FAQ)
Q1: What if I only know the total length of all three sides?
A1: Knowing only the total length is insufficient to determine individual side lengths. You need at least one individual measurement or a relationship between the sides to solve the problem.
Q2: Can I use this method for other ratios, like 2:5:7?
A2: Absolutely! The methods described work for any ratio. Just replace the 1:3:4 with your specific ratio and follow the same steps.
Q3: What if my ratio involves fractions?
A3: Treat fractions as you would any other number. For instance, if the ratio is 1/2:1:2, you would still apply the scale factor to each part of the ratio (after perhaps converting the fractions to decimals for easier calculation).
Q4: Are there any online tools to help with this conversion?
A4: While there aren't dedicated tools for this specific type of conversion (ratio to mm), general proportion calculators or unit converters can assist in some steps of the calculation. However, understanding the underlying principles is more valuable than relying on automated tools.
Conclusion
Converting a ratio like 1:3:4 into millimeter measurements involves understanding the concept of proportions and scale. By establishing a known measurement, you can determine the actual sizes of all dimensions. Whether you use the proportional method or the scale factor method, the key is to systematically apply the ratio to obtain the desired millimeter measurements. Remember that accuracy is crucial in many applications, so double-check your calculations and ensure you're using the correct units throughout the process. Mastering this conversion skill will enhance your ability to work with blueprints, models, and various design projects.
Latest Posts
Latest Posts
-
99 3 Fahrenheit To Celsius
Sep 15, 2025
-
Cuantos Gramos Es Media Libra
Sep 15, 2025
-
50 Grados Centigrados A Farenheit
Sep 15, 2025
-
Convert 49 C To F
Sep 15, 2025
-
Meters Cubed To Cubic Yards
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 3 4 To Mm . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.